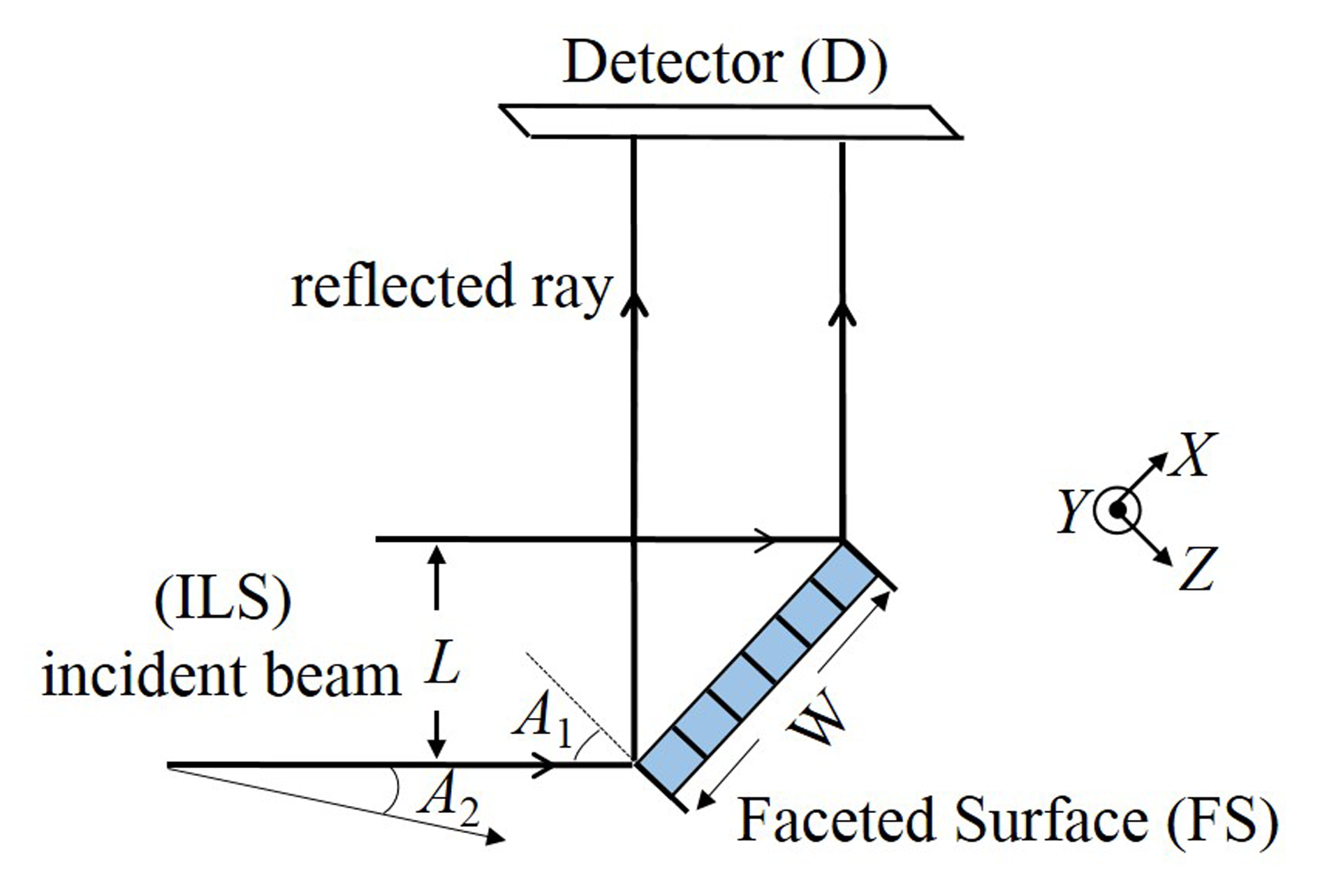
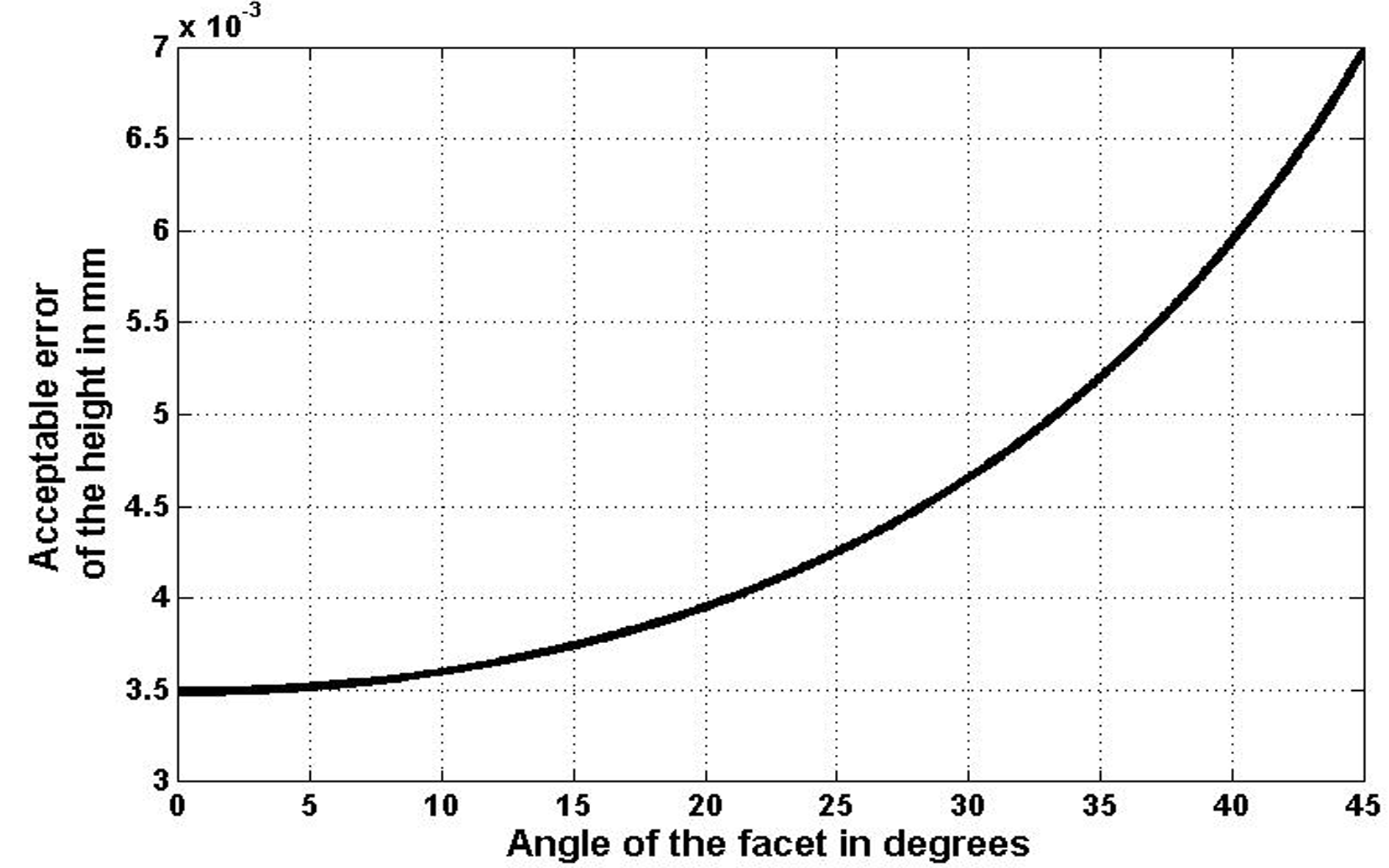
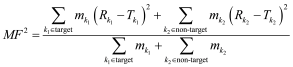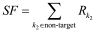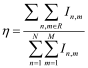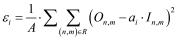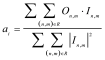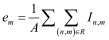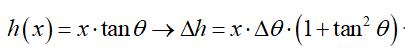For measuring the quality of the achieved irradiance distribution on the detector, numerical calculation is done with these four factors: the efficiency, the root mean square error, the uniformity and the correlation coefficient.
The efficiency η is given by Equation (3):
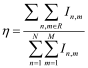 (3)
(3)In Equation (3), In,m is the actual irradiance distribution on the detector. R is the target area. N and M are the one-dimensional number of pixels on detector. In our case, N = M = 200. The efficiency η is the ratio of optical power in the target area to the total incidence power on the detector: it is a measurement of the useful energy in the irradiance map. In our case, we consider in the calculation any other energy losses as the reflective coefficient or roughness.
The root mean square error
εi is given in Equation (4) for measuring a mathematical distance between the target and the achieved irradiance distribution
[13, 14].
A is the number of pixels in the target area
R.
On,m is the desired irradiance distribution. The term
ai is a constant that normalizes the calculated irradiance map in order to get consistent error values. The root mean square error in intensity is the most straightforward criterion to evaluate the quality result, and thus the convergence rate of the optimization process. The equation is given by:
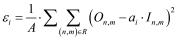 (4)
(4)where
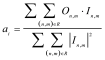 (5)
(5)The uniformity
U is given by Equation (6), which is the standard deviation of the difference between the actual irradiance and the mean irradiance
em[14] :
 (6)
(6)with the value em is the average of the irradiance in the target area:
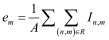 (7)
(7)The illumination uniformity
U is small if the difference between irradiance at each point and the mean value
em is small. Bokor et al. provide an equation for measuring the fidelity of an achieved irradiance distribution
[13-15]. They introduce a mathematical quantity which measures the correlation between the calculated irradiance map and the desired irradiance. This correlation coefficient is always in the interval [0,1] The expression of the correlation coefficient
C is given in the reference
[13].
The quality factors will be used in the following sections to measure the quality of the irradiance distribution on the detector and evaluate the influence of several important parameters on the reshaping result of the incoherent beam. These four factors contain the required information to analyze the irradiance map properties. It is important to note that the analysis in the next section should always be done by observing the 4 criteria together. Indeed, one can easily notice that the behaviour of efficiency and correlation coefficient are linked together, and so are also the uniformity and the error.
Of course, in some applications, factors are more relevant than others, for example uniformity in high quality illumination. The most important in studying the quality factor is to observe the evolution of these values in a large interval, knowing that only efficiency is possible to link to the experiment and easily measurable.